This feature interpolates the transformations of input matrices associated with the reference mesh onto the target mesh. It’s useful for transferring the location and orientation of elements like rig controllers, joints, or attachment points between different meshes, even if they have different topologies.
For each input matrix provided, two corresponding output matrix transformations are calculated:
- Matched Output (Static): This output represents the transformation of the input matrix mapped onto the undeformed target mesh. It calculates the input matrix’s position and orientation relative to the undeformed reference mesh and finds the equivalent transformation on the base target mesh. Example: If you associate an input matrix with the nose tip of a reference head mesh, this output will represent a transform positioned on the nose tip of the target head mesh. This output reflects changes to the input matrix, or the base meshes.
- Retargeted Output: This output calculates the transformation of the input matrix as it follows the deformation being transferred from the reference mesh to the target mesh. It uses the relationship between the undeformed reference mesh, a deformed version of the reference mesh, and the input matrix to drive the output matrix’s transformation relative to the node’s retargeted mesh output. This requires information from the deformed reference mesh and is essential when matrices need to dynamically follow retargeted deformations. Example: A joint driven by this output transformation would deform correctly along with the node’s retargeted mesh output.
Dynamic Updates: The feature updates dynamically. Moving the input matrices or changing the input geometries (reference, reference deformed, target) that drive the calculations will automatically update the corresponding output matrix transformations.
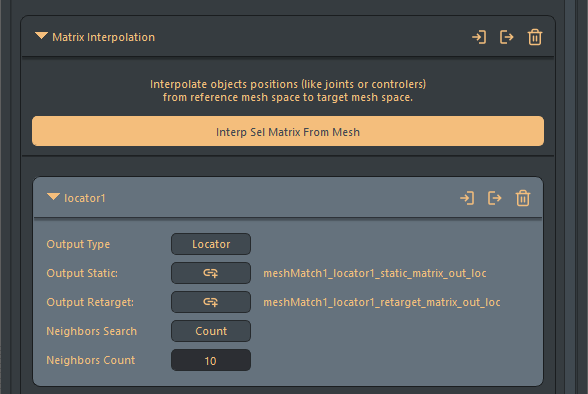
The UI is designed to create basic setup, but you can use the provided API to batch create all the interpolation for an entire complex rig. The UI will then be able to display and manage the in-out relationship.
Adding a Matrix:
- Using the UI: Open the Matrix section from the left panel. Then, select any transform object(s) from your scene that are tied to the reference mesh, and click on ‘Interp Sel Matrix From Mesh’ button.
- Using the python API or manually connect: For complex rigs, you can of course script all the connections setup using the provided API in ‘mesh_match_commands.py’ class, or manually plug any matrix attributes in-out. The UI will display all connections that have an input plug.
Per Matrix Section Features:
- Output type menu: You can use this menu to automatically create a locator in both outputs. Switching from ‘Locator’ to ‘Custom’, or adding a custom connection will delete the output locators.
- Output Static / Output Retarget: These lines display the current objects connected from the output attributes. Clicking on the ‘link’ button will offer to replace the current connected object with the current user selection.
Per Matrix Attributes:
- Neighbors Search:
Default: Count | options: Count/Distance Factor
This attribute determines how neighboring points on the reference mesh are identified for the interpolation calculation.. When set to ‘Count’, the interpolation algorithm will always use the n ‘Neighbors Count’ closest vertex position, regardless of the distance of this matrix. When set to ‘Radius Factor’, all the neighbors within the specified radius will be used, which can be more relevant if the mesh is really dense for example. - Neighbors Count:
Default: 10 | Min: 1 | Max: mesh total points
This parameter controls the amount of neighbors when neighbors search has been set to ‘Count’. - Radius Factor:
Default: 0.1 | Min: 0 | Max: 1
This parameter controls the distance from the input matrix in which neighbors are searched for.
Notes:- This 0-1 factor is internally remapped; a value of 1 corresponds to a world-space search distance of approximately 20% (0.2) of the reference mesh’s bounding box diagonal. This limit is based on the observation that searching further generally yields irrelevant results.
- A fallback mechanism has been implemented so that when no points have been found from this distance search, we use at least the 5 closest neighbors regardless of their distance.